What Are the Various Types of Recursions in Golang ?

As the title suggests, in this blog, we will focus on the concept of recursion in Golang. Like many other programming languages, Go also has recursion. Simply put, a recursion signifies a function calling itself repeatedly unless a base condition is fulfilled. However, it can be best understood with the help of a program. And we are going to do that here.
We are going to take the example of the most used program, that is, finding the factorial of a number.
The best part is that once you get familiar with the concept of recursion, it will help you out in writing intricate programs for Go development.
What is the Factorial of a Number?
Before we proceed to the program, we have to understand what the factorial of a number stands for.
So, we represent it simply like
n!= n* (n-1)* (n-2)* (n-3)* …..1
Thus, the factorial of a whole number can be defined as the function that leads to the multiplication of a number by every natural number that comes below it (i.e decrementing the value by 1).
For example, the factorial of 4 can be written as
4!= 4 * 3 * 2 * 1= 24.
Let’s Get Started with the Recursion Program
1. Direct Recursion
Here, I’ll be starting my program by creating a directory in the go -workspace. I’ll name this ‘recursion’. For that, I’ll type in the Command Prompt (or Terminal in the case of macOS or Linux)cd go-workspace
mkdir recursion
cd recursion
code .
When I type code ., the text editor opens up, i.e, the VS Code. You might have other IDEs or text editors at your disposal. In the VS Code, we will type:
package main
import (
“fmt”
)
func factorial (x int) int {
if x==1 || x== 0 {
return 1
}
return x* factorial (x-1)
}
func main() {
var x int
fmt.Scan (&x)
fmt.Println (factorial(x))
}
Ok, so let us understand the program. We have created a recursive function called factorial. func factorial (x int) int will accept a value of type integer and it will return an integer as well.
Next, we create a condition that if x is equal to 1 or o, it will return 1. So, we type:
if x==1|| x==0
return 1
However, if the condition is not true, then we type:
return x* factorial (x-1)
What we are essentially doing here is carrying out a multiplication and then calling the function. This is basically recursion, i.e, a function call is happening within the function itself.
Next, we proceed to function main. We create an input for x, So,
var int x
fmt.Scan (&x)
Then we print out the factorial by calling the function. When a function call occurs, a stack frame is created for each function call.
Output:

Point to Note: Whenever a recursive function call happens, the statement along with it gets stored inside the stack frame. This can be better understood with the help of a table below.
| fact (1) | 1 | Frame 3 |
|---|---|---|
| fact (2) | return 2 * fact (1) | Frame 2 |
| fact (3) | return 3 * fact (2) | Frame 1 |
| fact (4) | return 4 * fact (3) | Frame 0 |
Hopefully, you have understood the concept of recursive function. If you haven’t, then it is wise to take a look at examples online and compare them with the code explained here. You must be familiar with these topics in order to go about a smooth Go development process.
More Types of Recursion in Golang
Now, we will proceed to the different types of recursive functions. We have already covered the first one that is a direct recursion. We will take a look at the rest of them.
2. Indirect Recursion
A function (suppose ind) is called an indirect recursive if it calls upon another function (suppose ind2). Then the ind2 function will call the ind function indirectly or directly.
We will save this program in another Go source file titled ‘indirect.go’
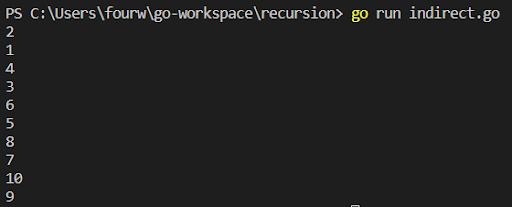
Let us take a look at an example. We will write a program to print the numbers from 1 to 10 in a particular manner such that when the number is odd, you have to add 1 and if it is even, then you have to subtract 1.
package main
import (
“fmt”
)
var n int
func odd() {
if (n <=10) {
fmt.Println ( n+1)
n++
even()
}
return
}
func even() {
if (n <=10) {
fmt.Println (n-1)
n++
odd()
}
return
}
func main() {
n=1
odd()
}
- Ok, let us understand what is going on in the program. We write a function odd(). We write an if statement. If n<=10, then it will print (n+1).
- As odd function will be handling odd numbers, so it will add 1 to the number. We then increment the value of n, so that it becomes an even number, and then we call even(). And we will return the values.
- The same logic applies for the even(). Since we will subtract 1 from even numbers, so we have included (n-1).
- Finally, we will be calling the function odd in the function main.
Output:
3. Tail Recursion
A recursive function is a tail recursive if it is the final or the last call of the function. In such recursions, there is actually no requirement to keep track of the previous state. In order to understand the concept, let us take an example. I’ll save this program inside a Go source file called ‘tail.go’
package main
import (
“fmt”
)
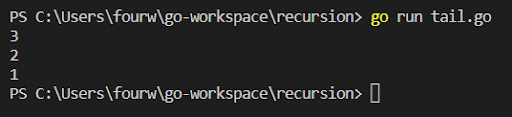
func tail (n int) {
if (n==0) {
return
}
fmt.Println (n)
tail (n-1)
}
func main () {
tail (3)
}
- Now, let us understand what this function has to say. The above program is a recursive program. This is because we are calling tail (n-1) within the function tail(n). However, this is a tail recursive program. Why? This is because the recursive call tail (n-1) is the final thing that has been performed by the function tail.
| tail(0) | return; |
|---|---|
| tail(1) | Act f1 |
| tail(2) | Act f2 |
| tail(3) | Act f3 |
| main() | Act m |
- Now, we have to evaluate the stack. The execution starts from the main function. Main function activation record will be stored first in the stack. Following this, we are calling tail(3) in the function main. So, the control will transfer from the main function to the tail(3). Here, n=3. So, we bypass the if condition. So the value 3 will get printed on the screen
- After the fmt.Println, we have another statement tail(n-1), Now this will simply call tail (2). So, the control will transfer from tail(3) to tail(2). The activation record of this function will be stored. Again, we bypass the if part. Next, the tail (n-1) part will be called, and this time it will be tail(1).
- Now, the control will be transferred from tail(2) to tail(1). And the activation record will be stored inside this step. So, the process will continue until n=0. Now that the condition is satisfied, it will simply return to the previous function tail(1).
- So, the activation record of tail(0) will get popped out of the stack. After this point, there is nothing to be evaluated. Hence, there is no requirement for keeping record of the previous state. This process will continue until the activation record for the main function gets popped out of the stack.
Output:
4. Head Recursion
In case of the head recursion, the function consists of the recursive call as the first statement. The general practice is that there should be no operation or statement before the recursive call. In the case of the head recursion, all the operations are carried out during the returning time. In this case, after returning back there is something to evaluate.
I'm saving this program in the Go source file titled ‘head.go’.
package main
import (
“fmt”
)
func head(n int) {
if (n==0) {
return
}
head (n-1)
fmt.Println (n)
}
func main() {
head(3)
}
- Let us try to understand this program with the help of a stack.
- The process of activation record being stored in the stack is similar to that of tail recursion. The execution will start from function main(). So, first, the activation record of main() function will be stored. The control will then transfer from main() to head(3). The process will continue until fun(0)
- Now that n==0, we will thus return. Here, we will go back to head(1), and the activation record of head(0) will be popped out of the stack. And the value of n will be printed at this instance (which is 1 now), since there is an operation following head(n-1).
- One by one the activation record of different functions will be popped. And the values will be printed.
Output:

5. Infinite Recursion
In the case of infinite recursion, there is no base case involved. So, the incursion occurs infinitely. This generally gives rise to memory overflow or system crashing. I’ll be saving this program in the Go source file ‘infinite.go’.
package main
import (
“fmt”
)
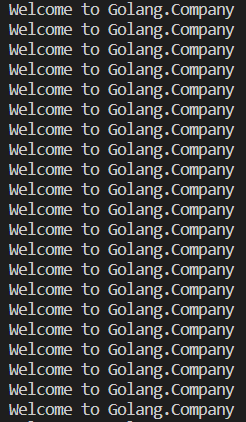
func infinite() {
fmt.Println (“Welcome to Golang.Company”)
infinite ()
}
func main(){
infinite ()
}
Here, we are writing an infinite recursive function with func infinite (). We are printing the statement and then calling the function inside the function itself. Since the main function executes the program. We are calling the infinite recursive function inside the function main.
Output:
6. Anonymous Function Recursion
As the name suggests, the anonymous functions have no names associated with it. It can be better understood with the help of an example. I’ll be saving this program in the Go source file named ‘anonymous.go’package main
import (
“fmt”
)
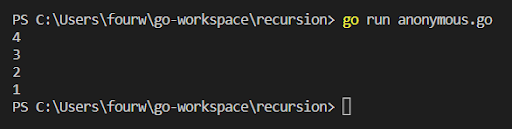
func main() {
var anon func (int)
anon= func (x int) {
if x==0 {
return
}
fmt.Println (x)
anon(x-1)
}
anon (4)
}
- Ok, it’s time to understand this program. We are starting with the main function. First, we are declaring the anonymous function var anon func (int) and it takes an integer value.
- Next, we are defining the anonymous function with the statement anon= func (x int). Following this, we are setting down the condition.
if x==0 {
return
}
fmt.Println (x)
anon(x-1)
}
- When the if condition is not satisfied, the value is printed and a call is made to anon (x-1). When we are writing anon(4), we are actually calling the anonymous recursive function.
Output:
Hopefully, you have understood the concept of recursion in Golang. However, it is imperative that you actually check out the codes by typing them out.
You will get full access to the codes on Github, at https://github.com/GolangCompany/recursion